Understanding Big O Notation: A Comprehensive Guide to Time Complexity (2025)

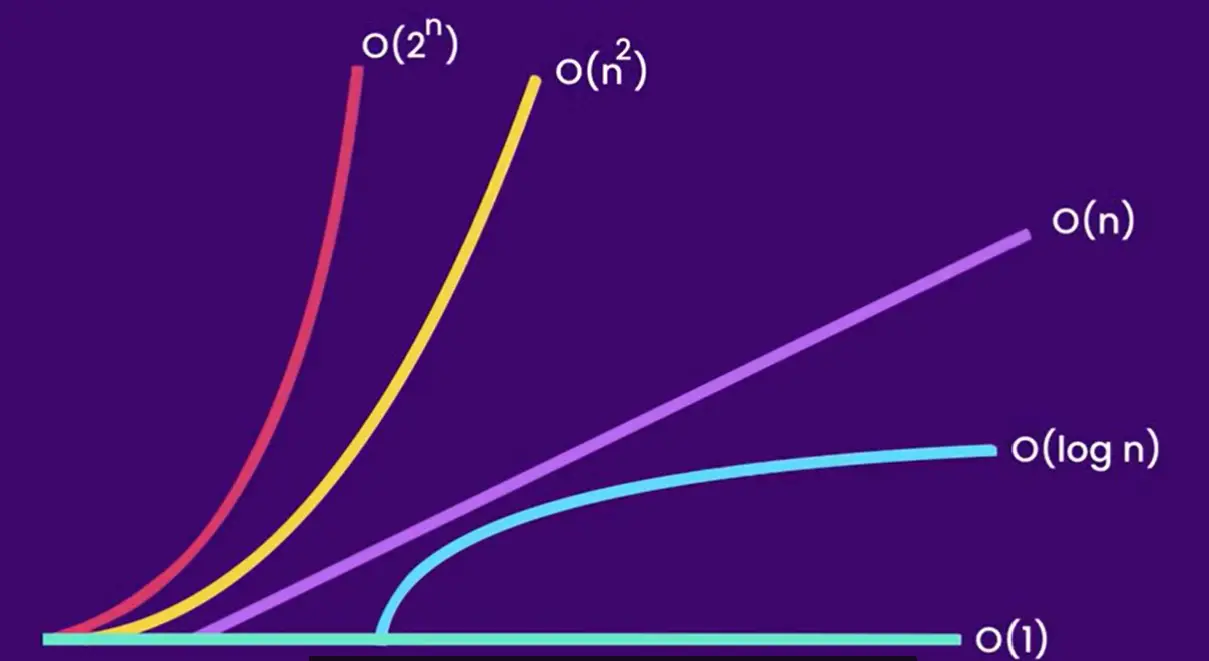
Big O notation is a fundamental concept in computer science that helps us understand and compare the efficiency of algorithms. This comprehensive guide explores different time complexities and their practical implications in software development.

Introduction to Big O Notation

Big O notation is a mathematical notation that describes the performance or complexity of an algorithm. It helps us understand how our code will scale as the input size grows. In simple terms, it tells us how fast an algorithm runs as the input size increases.

O(1) - Constant Time

Constant time complexity means the algorithm takes the same amount of time to execute regardless of the input size. These operations are extremely efficient and are the ideal choice when possible. Examples include accessing an array element by index or performing basic arithmetic operations.

Example of O(1) Operations

// O(1) - Accessing array element by index
public int getFirstElement(int[] array) {
    return array[0];
}

// O(1) - Basic arithmetic operations
public int add(int a, int b) {
    return a + b;
}

// O(1) - Hash map operations (average case)
public String getValue(Map map, String key) {
    return map.get(key);
}

O(n) - Linear Time

Linear time complexity indicates that the algorithm's execution time grows proportionally with the input size. If the input size doubles, the execution time also doubles. This is common in operations that need to process each element of an input once.

Example of O(n) Operations

// O(n) - Linear search
public int linearSearch(int[] array, int target) {
    for (int i = 0; i < array.length; i++) {
        if (array[i] == target) {
            return i;
        }
    }
    return -1;
}

// O(n) - Array traversal
public int sumArray(int[] array) {
    int sum = 0;
    for (int num : array) {
        sum += num;
    }
    return sum;
}

O(log n) - Logarithmic Time

Logarithmic time complexity is one of the most efficient complexities for large datasets. The execution time grows logarithmically with the input size, meaning it grows very slowly even as the input size increases dramatically. This is common in divide-and-conquer algorithms.

Example of O(log n) Operations

// O(log n) - Binary search
public int binarySearch(int[] array, int target) {
    int left = 0;
    int right = array.length - 1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (array[mid] == target) {
            return mid;
        }
        if (array[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return -1;
}

O(n²) - Quadratic Time

Quadratic time complexity means the execution time grows quadratically with the input size. If the input size doubles, the execution time quadruples. This is common in algorithms with nested loops and should be avoided for large datasets.

Example of O(n²) Operations

// O(n²) - Bubble sort
public void bubbleSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                // Swap elements
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
}

// O(n²) - Matrix multiplication
public int[][] multiplyMatrices(int[][] a, int[][] b) {
    int n = a.length;
    int[][] result = new int[n][n];
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            for (int k = 0; k < n; k++) {
                result[i][j] += a[i][k] * b[k][j];
            }
        }
    }
    return result;
}

O(2ⁿ) - Exponential Time

Exponential time complexity means the execution time grows exponentially with the input size. These algorithms become impractical very quickly as the input size increases. They are typically used only for small inputs or when no better solution exists.

Example of O(2ⁿ) Operations

// O(2ⁿ) - Recursive Fibonacci
public int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

// O(2ⁿ) - Subset generation
public List> generateSubsets(int[] nums) {
    List> subsets = new ArrayList<>();
    generateSubsetsHelper(nums, 0, new ArrayList<>(), subsets);
    return subsets;
}

private void generateSubsetsHelper(int[] nums, int index, 
                                 List current, 
                                 List> subsets) {
    subsets.add(new ArrayList<>(current));
    for (int i = index; i < nums.length; i++) {
        current.add(nums[i]);
        generateSubsetsHelper(nums, i + 1, current, subsets);
        current.remove(current.size() - 1);
    }
}

Best Practices and Optimization

Optimization Strategies

• Use appropriate data structures for your use case
• Implement caching when possible
• Break down complex problems into smaller, more manageable parts
• Consider space-time trade-offs
• Use built-in optimized functions when available
• Profile your code to identify bottlenecks

Conclusion

Understanding Big O notation is essential for writing efficient code and building scalable applications. By analyzing time complexity, developers can make informed decisions about algorithm selection and optimization strategies. Remember that choosing the right algorithm can significantly impact your application's performance, especially when dealing with large datasets.